最近學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)，對于從未接觸過數(shù)據(jù)結(jié)構(gòu)的我來說，老師不僅講解理論，還有代碼的逐層分析，非常不錯(cuò)，受益匪淺！！！（以下是學(xué)習(xí)記錄）

黑馬程序員孔德海老師教程

目錄

• 重點(diǎn)+基礎(chǔ)語法
• 時(shí)間復(fù)雜度(主要關(guān)注最壞時(shí)間復(fù)雜度)
• time.it，list，dic內(nèi)置函數(shù)
• 數(shù)據(jù)結(jié)構(gòu)
• 順序表
• • 順序表的2個(gè)形式
  • 順序表的結(jié)構(gòu)與實(shí)現(xiàn)
  • 順序表數(shù)據(jù)區(qū)擴(kuò)充
  • 順序表的操作
  • python_list使用順序表數(shù)據(jù)結(jié)構(gòu)
• 鏈表
• • 單鏈表的實(shí)現(xiàn)
  • • 指定位置添加元素
    • 查找節(jié)點(diǎn)是否存在
    • 刪除節(jié)點(diǎn)
  • 鏈表與順序表的對比
  • 雙向鏈表
  • 單向循環(huán)鏈表
  • • length(self)返回鏈表長度
    • 頭部添加節(jié)點(diǎn)
• 棧
• 隊(duì)列
• 排序
• • 冒泡排序O(n2)穩(wěn)定
  • 選擇排序O(n2)不穩(wěn)定
  • 插入排序O(n2)穩(wěn)定
  • 希爾排序
  • 快速排序(不穩(wěn)定)
  • 歸并排序
  • 排序算法效率比較
• 搜索
• 樹
• • 樹的存儲
  • 應(yīng)用
  • 二叉樹的節(jié)點(diǎn)表示以及樹的創(chuàng)建
  • 二叉樹的遍歷
  • • 廣度優(yōu)先遍歷(層次遍歷)
    • 深度優(yōu)先遍歷
  • 根據(jù)數(shù)據(jù)畫樹圖
• 樹的補(bǔ)充
• • 二叉排序樹（BST）
  • 平衡二叉樹（AVL）
  • 紅黑樹
  • 多路查找樹
  • • B-樹（多路平衡查找樹）
    • B+樹

重點(diǎn)+基礎(chǔ)語法

python語言只要是給出的變量名，里邊存儲的都是地址值(可以把類，函數(shù)，付給變量a)。
如a=5 a=“s” a=Person() a=f 方法

java基本數(shù)據(jù)類型中，變量a存放的是數(shù)值。引用數(shù)據(jù)類型(對象，數(shù)組，集合)的變量a存放的是地址。

#1 strat=time.time()

時(shí)間復(fù)雜度(主要關(guān)注最壞時(shí)間復(fù)雜度)

不同方法間的復(fù)雜度

import time start= time.time() for i in range(0,1001):for j in range(0,1001):for k in range(0,1001):if i+j+k==1000 and i**2+j**2==k**2:print(i,j,k) end = time.time() print("總開銷：",end-start)#總開銷： 126.49699997901917start1= time.time() for i in range(0,1001):for j in range(0,1001):k=1000-i-jif i**2+j**2==k**2:print(i,j,k) end1= time.time() print("總開銷：",end1-start1)#總開銷： 1.0120000839233398

T(n)時(shí)間復(fù)雜度，n執(zhí)行的步數(shù)
大O表示法，只記錄最顯著特征O(n)=nxn

最壞時(shí)間復(fù)雜度（平常說的就是這個(gè)）
比如對一個(gè)list排序，無序的復(fù)雜度要高于有序

基本步驟：順序，條件(取T最大值)，循環(huán)
li.append()不能看成一步，只有分析函數(shù)中的封裝才能看到append的時(shí)間復(fù)雜度

time.it，list，dic內(nèi)置函數(shù)

from timeit import Timer def test3():l = [i for i in range(1000)] t3 = Timer("test3()", "from __main__ import test3")#1函數(shù)名，2import，因?yàn)檫@個(gè)Timer不一定在這里運(yùn)行 print("comprehension ",t3.timeit(number=10000), "seconds")#test3()執(zhí)行10000次后，10000次總的執(zhí)行時(shí)間import time start=time.time()#從1970年到現(xiàn)在的計(jì)時(shí)秒數(shù) end=time.time()-start#返回秒

對于上例使用不同方法實(shí)現(xiàn)時(shí)

1. ('list(range(1000)) ', 0.014147043228149414, 'seconds') ('l = [i for i in range(1000)]', 0.05671119689941406, 'seconds') ('li.append ', 0.13796091079711914, 'seconds') ('concat加 ', 1.7890608310699463, 'seconds') 2.由于數(shù)據(jù)的存儲方式不同，導(dǎo)致插頭部和尾部 append()#2.159s insert(0,i)#30.00s pop(end)#0.00023,對尾部彈出 pop(0)#1.91

數(shù)據(jù)結(jié)構(gòu)

數(shù)據(jù)是一個(gè)抽象的概念，將其分類后得到程序語言的基本類型，如int,float,char。數(shù)據(jù)結(jié)構(gòu)指對數(shù)據(jù)的一種封裝組成，如高級數(shù)據(jù)結(jié)構(gòu)list，字典。數(shù)據(jù)結(jié)構(gòu)就是一個(gè)類的概念，數(shù)據(jù)結(jié)構(gòu)有順序表、鏈表、棧、隊(duì)列、樹。

算法復(fù)雜度只考慮的是運(yùn)行的步驟，數(shù)據(jù)結(jié)構(gòu)要與數(shù)據(jù)打交道。數(shù)據(jù)保存的方式不同決定了算法復(fù)雜度

程序 = 數(shù)據(jù)結(jié)構(gòu) + 算法
總結(jié)：算法是為了解決實(shí)際問題而設(shè)計(jì)的，數(shù)據(jù)結(jié)構(gòu)是算法需要處理的問題載體

抽象數(shù)據(jù)類型(Abstract Data Type)
抽象數(shù)據(jù)類型(ADT)的含義是指一個(gè)數(shù)學(xué)模型以及定義在此數(shù)學(xué)模型上的一組操作。

== 代碼編寫注意==

2.對于鏈表要先接入新的node，再打斷原來的，要注意順序

下面講的各種表都是一種數(shù)據(jù)的封裝結(jié)構(gòu)

順序表

順序表+鏈表=線性表：一根線串起來，兩種表都是用來存數(shù)據(jù)的

順序表的2個(gè)形式

計(jì)算機(jī)存儲
計(jì)算機(jī)最小尋址單位是1字節(jié)，就是一個(gè)字節(jié)，才有一個(gè)地址，所有的地址都是統(tǒng)一大小0x27 4個(gè)字節(jié)

元素內(nèi)置順序表
對于存放一個(gè)含有相同類型元素的list來講，用順序表封裝成一個(gè)數(shù)據(jù)結(jié)構(gòu)。

元素外置順序表

元素內(nèi)置順序表，是指存儲的數(shù)據(jù)類型都是一樣，這樣為每個(gè)元素開辟的空間都是一樣大的，在根據(jù)index找元素的時(shí)候
如list1=[1,2,3], 可以根據(jù)list的首地址0x12，很容易計(jì)算要查詢元素的物理地址=0x12+index x 4.
元素外置, 指存的數(shù)據(jù)類型不一樣，如list2=[1,3,“b”,4,“ccc”]

順序表的結(jié)構(gòu)與實(shí)現(xiàn)

對于python來講已經(jīng)做好封裝，不需要寫容量，元素個(gè)數(shù)


so常用的是分離式

順序表數(shù)據(jù)區(qū)擴(kuò)充

如果數(shù)據(jù)要來回增，刪，導(dǎo)致空間不穩(wěn)定，所以有了策略

順序表的操作

python_list使用順序表數(shù)據(jù)結(jié)構(gòu)

1.表頭與數(shù)據(jù)分離式 2.因?yàn)橐粋€(gè)list中有int，也有字符所以用的是元素外置 3.動態(tài)順序中的倍數(shù)擴(kuò)充

鏈表

# cur做判斷，邏輯(不是指針)走到最后一個(gè)元素時(shí)，里面的方法體是執(zhí)行的 # 用cur.next做判斷，while循環(huán)中是不執(zhí)行的 # 如果發(fā)現(xiàn)少一次執(zhí)行語句，可以手動打印，就不用完全在while循環(huán)中執(zhí)行

java，c語言是需要中間變量temp，才能完成交換，只有python可以直接交換

單鏈表的實(shí)現(xiàn)

cur：指針地址
cur.elment:地址中的元素
cur=self._head先提出等式右邊地址，再給cur

多寫幾次單鏈表，有助理解，鏈表的運(yùn)行過程

1. """單鏈表的結(jié)點(diǎn)，里面存放element區(qū)和next"""相當(dāng)于元祖（element，next） class SingleNode(object):def __init__(self,item):# _item存放數(shù)據(jù)元素self.item = item# _next是下一個(gè)節(jié)點(diǎn)的標(biāo)識self.next = None 2."""單鏈表數(shù)據(jù)結(jié)構(gòu)類，具有以下功能"""相當(dāng)于python中的list數(shù)據(jù)結(jié)構(gòu)類，同時(shí)它也具有以下功能 class SingleLinkList(object):"""存放一個(gè)屬性P，好用來指向第一個(gè)節(jié)點(diǎn)"""def __init__(self，):self._head = None# _ 私有屬性,head=None說明P指向的單鏈表中沒有nodedef is_empty(self):"""判斷鏈表是否為空"""return self._head == Nonedef length(self):"""鏈表長度"""# current游標(biāo)用來遍歷節(jié)點(diǎn)，初始時(shí)指向頭節(jié)點(diǎn)cur = self._head#直接指到第一個(gè)節(jié)點(diǎn)count = 0# 尾節(jié)點(diǎn)指向None，當(dāng)未到達(dá)尾部時(shí)while cur != None:count += 1# 將cur后移一個(gè)節(jié)點(diǎn)cur = cur.next #相當(dāng)于指向下一個(gè)節(jié)點(diǎn)return countdef travel(self):"""遍歷鏈表"""cur = self._head#直接指到第一個(gè)節(jié)點(diǎn)while cur != None:print cur.item,#打印第一個(gè)節(jié)點(diǎn)cur = cur.next#相當(dāng)于指向下一個(gè)節(jié)點(diǎn)print ""def add(self, item):"""頭部添加元素"""# 先創(chuàng)建一個(gè)保存item值的節(jié)點(diǎn)node = SingleNode(item)# 將新節(jié)點(diǎn)的鏈接域next指向頭節(jié)點(diǎn)，即_head指向的位置,有先后，否則會丟失鏈node.next = self._head# 將鏈表的頭_head指向新節(jié)點(diǎn)self._head = nodedef append(self, item):"""尾部添加元素"""node = SingleNode(item)# 先判斷鏈表是否為空，若是空鏈表，則將_head指向新節(jié)點(diǎn)if self.is_empty():self._head = node#append時(shí)候，我只要保證把我的node地址給你就行，node.next不用管# 若不為空，則找到尾部，將尾節(jié)點(diǎn)的next指向新節(jié)點(diǎn)else:cur = self._headwhile cur.next != None:cur = cur.nextcur.next = node#直接將node送給cur.next，內(nèi)部操作就是把node結(jié)點(diǎn)地址給他if __name__=="__main__":li=SingleLinkList()print(li.is_empty())print(li.length())node = SingleNode(3)li.append(11111)li.travel()3.使用node =Node(100)single_obj=SingleLinkList(node)#創(chuàng)建node，讓單鏈表指向它single_obj=SingleLinkList()#直接創(chuàng)建空鏈表

指定位置添加元素


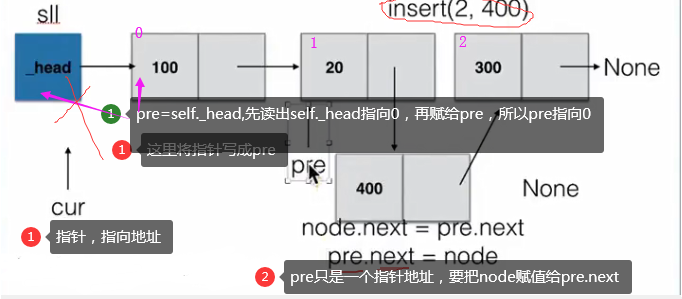
def insert(self, pos, item):"""指定位置添加元素"""# 若指定位置pos為第一個(gè)元素之前，則執(zhí)行頭部插入if pos <= 0:self.add(item)# 若指定位置超過鏈表尾部，則執(zhí)行尾部插入elif pos > (self.length()-1):self.append(item)# 找到指定位置else:node = SingleNode(item)count = 0# pre用來指向指定位置pos的前一個(gè)位置pos-1，初始從頭節(jié)點(diǎn)開始移動到指定位置pre = self._headwhile count < (pos-1):count += 1pre = pre.next# 先將新節(jié)點(diǎn)node的next指向插入位置的節(jié)點(diǎn)node.next = pre.next# 將插入位置的前一個(gè)節(jié)點(diǎn)的next指向新節(jié)點(diǎn)pre.next = node

查找節(jié)點(diǎn)是否存在

def search(self,item):"""鏈表查找節(jié)點(diǎn)是否存在，并返回True或者False"""cur = self._headwhile cur != None:#一直往后走，起到遇到none停止if cur.item == item:return Truecur = cur.nextreturn False

刪除節(jié)點(diǎn)

def remove(self,item):"""刪除節(jié)點(diǎn)"""cur = self._headpre = Nonewhile cur != None:# 找到了指定元素if cur.item == item:# 如果第一個(gè)就是刪除的節(jié)點(diǎn)if not pre:# 將頭指針指向頭節(jié)點(diǎn)的后一個(gè)節(jié)點(diǎn)self._head = cur.nextelse:# 將刪除位置前一個(gè)節(jié)點(diǎn)的next指向刪除位置的后一個(gè)節(jié)點(diǎn)pre.next = cur.nextbreakelse:# 繼續(xù)按鏈表后移節(jié)點(diǎn)pre = curcur = cur.next

鏈表與順序表的對比

鏈表只能記錄頭節(jié)點(diǎn)地址，因此在訪問，尾部插，中間查時(shí)，都需要從頭節(jié)點(diǎn)，遍歷過去，所以復(fù)雜度O(n)

鏈表可以利用離散的空間，順序表只能開辟完整的連續(xù)空間，只要list不夠，必須重新開辟

鏈表時(shí)間花費(fèi)到遍歷地址上，順序表花費(fèi)到表的復(fù)制搬遷

雙向鏈表

對于前面單向的，當(dāng)前node不能查看其前面node的信息，所以引入雙向。添加，刪除node時(shí)，要保證每個(gè)node中的P,N都 給上值，如：中間插入

頭部插入元素

def add(self, item):"""頭部插入元素"""node = Node(item)if self.is_empty():# 如果是空鏈表，將_head指向nodeself._head = nodeelse:# 將node的next指向_head的頭節(jié)點(diǎn)node.next = self._head# 將_head的頭節(jié)點(diǎn)的prev指向nodeself._head.prev = node# 將_head 指向nodeself._head = node

尾部插入元素

def append(self, item):"""尾部插入元素"""node = Node(item)if self.is_empty():# 如果是空鏈表，將_head指向nodeself._head = nodeelse:# 移動到鏈表尾部cur = self._headwhile cur.next != None:cur = cur.next# 將尾節(jié)點(diǎn)cur的next指向nodecur.next = node# 將node的prev指向curnode.prev = cur

中間插入

單向循環(huán)鏈表

由于是循環(huán)列表，最后的尾結(jié)點(diǎn)不再是None結(jié)束，而是指向self._head
由于一開始將cur = self._head設(shè)成游標(biāo)，所以判斷語句只能是cur.next
while cur.next != self._head
使用cur.next不能進(jìn)到循環(huán)體，會導(dǎo)致少一次打印，可以手動打印

length(self)返回鏈表長度

def length(self):"""返回鏈表的長度"""# 如果鏈表為空，返回長度0if self.is_empty():return 0count = 1cur = self._head#指針啟動地址while cur.next != self._head:#因?yàn)檠h(huán)鏈表最后一個(gè)node要帶有self._head，所以通過判斷是否有self._head來看是否一個(gè)循環(huán)結(jié)束count += 1cur = cur.nextreturn count

頭部添加節(jié)點(diǎn)

def add(self, item):"""頭部添加節(jié)點(diǎn)"""node = Node(item)if self.is_empty():self._head = nodenode.next = self._headelse:#添加的節(jié)點(diǎn)指向_headnode.next = self._head# 移到鏈表尾部，將尾部節(jié)點(diǎn)的next指向nodecur = self._headwhile cur.next != self._head:cur = cur.nextcur.next = node#_head指向添加node的self._head = node

棧

棧=杯
順序表，鏈表是用來存數(shù)據(jù)的
棧和隊(duì)列不考慮數(shù)據(jù)是如何存放的，棧stack，隊(duì)列是一種容器，執(zhí)行什么樣的操作，抽象結(jié)構(gòu)。
6*（2+3）

#利用前面封裝好的順序表的二次開發(fā) class Stack(object):"""棧"""def __init__(self):#初始化的時(shí)候要生成一個(gè)容器，順序表就是python中的list，然后再執(zhí)行操作，可將list設(shè)成私有的，self.__items = []這樣就不能修改原來的list容器self.items = []def is_empty(self):"""判斷是否為空"""return self.items == []#右邊是一個(gè)判斷返回True#對于存放的數(shù)據(jù)結(jié)構(gòu)是順序表來講，尾部壓棧出棧復(fù)雜度為o（1），對于鏈表來講，頭部復(fù)雜度為o（1），所以要考慮def push(self, item):#從尾部壓，從尾部取"""加入元素"""self.items.append(item)def pop(self):"""彈出元素"""return self.items.pop()def peek(self):"""返回棧頂元素"""return self.items[len(self.items)-1]def size(self):"""返回棧的大小"""return len(self.items)if __name__ == "__main__":stack = Stack()stack.push("hello")stack.push("world")stack.push("itcast")print stack.size()print stack.peek()print stack.pop()print stack.pop()print stack.pop()

隊(duì)列

#因?yàn)槌鋈腙?duì)總有一個(gè)復(fù)雜度為N,所以考慮是出隊(duì)用的多，還是入隊(duì)多，再寫程序 class Queue(object):"""隊(duì)列"""def __init__(self):#空列表保存隊(duì)列self.items = []def is_empty(self):return self.items == []def enqueue(self, item):"""進(jìn)隊(duì)列"""self.items.insert(0,item)def dequeue(self):"""出隊(duì)列"""return self.items.pop()def size(self):"""返回大小"""return len(self.items)if __name__ == "__main__":q = Queue()q.enqueue("hello")q.enqueue("world")q.enqueue("itcast")print q.size()print q.dequeue()print q.dequeue()print q.dequeue()

雙端隊(duì)列
兩個(gè)棧尾部放一起

是上面的擴(kuò)展，含有的函數(shù)功能更多了

排序

排序算法的穩(wěn)定性

冒泡排序O(n2)穩(wěn)定

#可以將這個(gè)算法操作在順序表上（改變存儲位置），也可以操作在鏈表上（改變node節(jié)點(diǎn)） #不論list是什么要，O（n）=n^2 def bubble_sort(alist):for j in range(len(alist)-1,0,-1):#n-1,n-2,,,1# j表示每次遍歷需要比較的次數(shù)，是逐漸減小的for i in range(j):if alist[i] > alist[i+1]:alist[i], alist[i+1] = alist[i+1], alist[i]li = [54,26,93,17,77,31,44,55,20] bubble_sort(li) print(li)#加個(gè)檢測是否交換的優(yōu)化的count,這樣復(fù)雜度為n #[1,2,3,4,5,9,8] def bubble_sort(alist):for j in range(len(alist)-1,0,-1):#n-1,n-2,,,1# j表示每次遍歷需要比較的次數(shù)，是逐漸減小的count=0for i in range(j):if alist[i] > alist[i+1]:alist[i], alist[i+1] = alist[i+1], alist[i]count+=1if 0 == count:contine li = [54,26,93,17,77,31,44,55,20] bubble_sort(li) print(li)

冒泡是穩(wěn)定的

選擇排序O(n2)不穩(wěn)定

比如[5,5,2],就是不穩(wěn)定的
選擇排序，插入排序，希爾排序是把序列分成兩部分，把其中的一部分元素往另外一部分做

list=[54,226,93,17,77,31,44,55,21] def selec_sort(list):for j in range(len(list)-1):min=list[j]for i in range(j+1,len(list)):if list[i]<min:min=list[i]list[j],list[i]=list[i],list[j]print(list) selec_sort(list)

插入排序O(n2)穩(wěn)定

#這個(gè)想法像選擇排序，每次對比選出最大，沒有插序的相鄰之間對比，向前移 list=[54,226,93,17,77,44,4,55,21]#0, 1, 2, 3 4, 5, 6 ,7, 8 def insert_sort(list):for j in range(1,len(list)):max=list[j]for i in range(0,len(list)-1,1):#先寫第一個(gè)循化，可以直接用下表list[1],然后再加上外循環(huán)，看看j與list[1]下標(biāo)的關(guān)系if list[i]>max:max=list[i]list[j],list[i]=list[i],list[j]print(list) insert_sort(list) #version1插序的相鄰之間對比，向前移，用下面的方法 def insert_sort(alist):# 從第二個(gè)位置，即下標(biāo)為1的元素開始向前插入for i in range(1, len(alist)):# 從第i個(gè)元素開始向前比較，如果小于前一個(gè)元素，交換位置for j in range(i, 0, -1):if alist[j] < alist[j-1]:alist[j], alist[j-1] = alist[j-1], alist[j]alist = [54,26,93,17,77,31,44,55,20] insert_sort(alist) print(alist)#version2 #對于上面的用for j in range(i, 0, -1):來控制i，與i-1，i-2的比較，操作比較復(fù)雜 #這里用 while i>0: i-=1 來控制指針向0的方向移動，隨著i的變動，每次只比較i與i-1 def insert_sort(alist):# 從第二個(gè)位置，即下標(biāo)為1的元素開始向前插入for i in range(1, len(alist)):# 從第i個(gè)元素開始向前比較，如果小于前一個(gè)元素，交換位置while i>0:if alist[i] < alist[i-1]:alist[i], alist[i-1] = alist[i-1], alist[i]i-=1else:break alist = [54,26,93,1711,77,31,44,55,20] insert_sort(alist) print(alist)

希爾排序

def shell_sort(list):n=len(list)gap=n//2 #gap=4while gap>=1:#gap一直變化到1for j in range(gap,n):#for控制的是gap=4時(shí)的4個(gè)子序列i=jwhile i >0:#跟之前插入排序一樣，對于一個(gè)序列的具體操作，與普通插入的區(qū)別就是gap步長if list[i]<list[i-gap]:list[i],list[i-gap]=list[i-gap],list[i]i-=gapelse:breakgap//=2#gap減半list = [54,26,93,17,77,31,44,55,20] shell_sort(list) print(list)

快速排序(不穩(wěn)定)

快速排序（英語：Quicksort），又稱劃分交換排序（partition-exchange sort），通過一趟排序?qū)⒁判虻臄?shù)據(jù)分割成獨(dú)立的兩部分，其中一部分的所有數(shù)據(jù)都比另外一部分的所有數(shù)據(jù)都要小，然后再按此方法對這兩部分?jǐn)?shù)據(jù)分別進(jìn)行快速排序，整個(gè)排序過程可以遞歸進(jìn)行，以此達(dá)到整個(gè)數(shù)據(jù)變成有序序列。
注意
1.version2 中，兩個(gè)while有一個(gè)是等號，保證相同大小的元素放到mid的同一邊，這是快排設(shè)計(jì)的一個(gè)思想
用version2的思想寫代碼

def quick_sort(alist, start, end):"""快速排序"""# 遞歸的退出條件if start >= end:return# 設(shè)定起始元素為要尋找位置的基準(zhǔn)元素mid = alist[start]# low為序列左邊的由左向右移動的游標(biāo)low = start# high為序列右邊的由右向左移動的游標(biāo)high = endwhile low < high:# 如果low與high未重合，high指向的元素不比基準(zhǔn)元素小，則high向左移動while low < high and alist[high] >= mid:#加=號表示將2個(gè)一樣的值放到一邊，不加的話，最終迭代后也會正確high -= 1# 將high指向的元素放到low的位置上alist[low] = alist[high]# 如果low與high未重合，low指向的元素比基準(zhǔn)元素小，則low向右移動while low < high and alist[low] < mid:low += 1# 將low指向的元素放到high的位置上alist[high] = alist[low]# 退出循環(huán)后，low與high重合，此時(shí)所指位置為基準(zhǔn)元素的正確位置# 將基準(zhǔn)元素放到該位置alist[low] = mid# 對基準(zhǔn)元素左邊的子序列進(jìn)行快速排序quick_sort(alist, start, low-1)#這里要保證使用同一個(gè)list，這樣產(chǎn)生的多個(gè)子序列下標(biāo)是保持不變的，才能恢復(fù)成一個(gè)list# 對基準(zhǔn)元素右邊的子序列進(jìn)行快速排序quick_sort(alist, low+1, end)alist = [54,26,93,17,77,31,44,55,20] quick_sort(alist,0,len(alist)-1) print(alist)

歸并排序

def merge_sort(alist):if len(alist) <= 1:#遞歸的終止條件 return alist# 二分分解num = len(alist)/2left = merge_sort(alist[:num]) right = merge_sort(alist[num:])# 合并return merge(left,right)def merge(left, right):'''合并操作，將兩個(gè)有序數(shù)組left[]和right[]合并成一個(gè)大的有序數(shù)組'''#left與right的下標(biāo)指針l, r = 0, 0result = []while l<len(left) and r<len(right):if left[l] < right[r]:result.append(left[l])l += 1else:result.append(right[r])r += 1result += left[l:]#當(dāng)上面的while循環(huán)出來時(shí)，一個(gè)list的元素是取完的，保證將另外一個(gè)list余下的元素appendresult += right[r:]return result#是一個(gè)新list，不再使用之前l(fā)ist下標(biāo)alist = [54,26,93,17,77,31,44,55,20] sorted_alist = mergeSort(alist) print(sorted_alist)

遞歸時(shí)要注意縮進(jìn)，這樣可以幫助理解

排序算法效率比較

搜索

二分法
前提，二分查找只能作用于有序列表

遞歸法：當(dāng)list處理后得到的list，還想再進(jìn)行同樣的操作，使用遞歸，但是不能無限遞歸下去，所以終止條件很重要，在這個(gè)例子中，要么alist[midpoint]=item，return True，要么 if len(alist) = 0: return False，用來退出遞歸

#遞歸法，每次生成一個(gè)新的list def binary_search(alist, item):if len(alist) == 0:return Falseelse:midpoint = len(alist)//2if alist[midpoint]==item:return Trueelse:if item<alist[midpoint]:return binary_search(alist[:midpoint],item)else:return binary_search(alist[midpoint+1:],item)testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,] print(binary_search(testlist, 3)) print(binary_search(testlist, 13))binary_search([0, 1, 2, 8, 13, 17, 19, 32, 42,],item=3)midpoint=43<13binary_search([0, 1, 2, 8],item=3)midpoint=23>2binary_search([8],item=3)midpoint=1//2=03<8binary_search([],item=3)#a=[1,2,3,4] print(a[5:])會返回空列表return False

非遞歸
遞歸法，調(diào)用函數(shù)自身,每次生成一個(gè)新的list,然后在list上操作.非遞歸法使用的是同一個(gè)list,所以first,last下標(biāo)很重要,在while循環(huán)中,不斷更新first,last值來實(shí)現(xiàn)對于list的取值控制

def binary_search(alist, item):first = 0last = len(alist)-1while first<=last:midpoint = (first + last)/2if alist[midpoint] == item:return Trueelif item < alist[midpoint]:last = midpoint-1else:first = midpoint+1return False testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,] print(binary_search(testlist, 3)) print(binary_search(testlist, 13))

樹

和前面的二分查找是一樣的

樹的存儲

應(yīng)用

二叉樹的節(jié)點(diǎn)表示以及樹的創(chuàng)建

self.root = root#保存一個(gè)根節(jié)點(diǎn),可以有,也可以沒有,如果有的話說明self.root后面跟著一串?dāng)?shù)據(jù),然后.append,在這個(gè)基礎(chǔ)上進(jìn)行加.如果self.root=None,self.root = node,為樹創(chuàng)建第一個(gè)節(jié)點(diǎn)

A為第一層，2^ 0, 2^1, ,2^2
寫完代碼后,要分析下特殊情況是否可以跑通,若不能的話,再寫特殊語句對待

廣度優(yōu)先的add實(shí)現(xiàn)的二茶樹->考察隊(duì)列，先入先出

#樹就是鏈表的擴(kuò)充,鏈表有一個(gè)element,和next,但是樹有兩個(gè)分支,所以lchild,rchild. class Node(object):"""節(jié)點(diǎn)類"""def __init__(self, elem, lchild=None, rchild=None):self.elem = elemself.lchild = lchildself.rchild = rchild#樹的創(chuàng)建,創(chuàng)建一個(gè)樹的類，并給一個(gè)root根節(jié)點(diǎn)，一開始為空，隨后添加節(jié)點(diǎn) class Tree(object):"""樹類"""def __init__(self, root=None):self.root = root#保存一個(gè)根節(jié)點(diǎn),可以有,也可以沒有,如果有的話說明self.root后面跟著一串?dāng)?shù)據(jù),然后.append,在這個(gè)基礎(chǔ)上進(jìn)行加.如果self.root=None,self.root = node,為樹創(chuàng)建第一個(gè)節(jié)點(diǎn)def add(self, elem):#廣度優(yōu)先的添加方式創(chuàng)建的二茶樹"""為樹添加節(jié)點(diǎn)"""node = Node(elem)#如果樹是空的，則對根節(jié)點(diǎn)賦值,若沒有這行,直接走到下面會出錯(cuò)if self.root == None:self.root = nodeelse:queue = []queue.append(self.root)#對已有的節(jié)點(diǎn)進(jìn)行層次遍歷while queue:# 通過不斷的壓入隊(duì)列，里面的數(shù)將會越來越多，不會為0#彈出隊(duì)列的第一個(gè)元素cur = queue.pop(0)if cur.lchild == None:cur.lchild = nodereturnelif cur.rchild == None:cur.rchild = nodereturnelse:#如果左右子樹都不為空，加入隊(duì)列繼續(xù)判斷queue.append(cur.lchild)queue.append(cur.rchild)

二叉樹的遍歷

廣度優(yōu)先遍歷(層次遍歷)

def breadth_travel(self):"""利用隊(duì)列實(shí)現(xiàn)樹的層次遍歷"""if self.root == None:returnqueue = []queue.append(root)while queue:#這個(gè)queue最后是要為空的（上面的那么add的queue，由于滿足條件就會return，所以不會空）node = queue.pop(0)print node.elem,if node.lchild != None:queue.append(node.lchild)if node.rchild != None:queue.append(node.rchild)

深度優(yōu)先遍歷

每次把框縮小一開始0為根節(jié)點(diǎn),然后1為根節(jié)點(diǎn),然后3為根節(jié)點(diǎn),根節(jié)點(diǎn)一直變動

def preorder(self, root):"""遞歸實(shí)現(xiàn)先序遍歷"""if root == None:#控制迭代結(jié)束returnprint root.elemself.preorder(root.lchild)self.preorder(root.rchilddef inorder(self, root): """遞歸實(shí)現(xiàn)中序遍歷"""if root == None:returnself.inorder(root.lchild)print root.elemself.inorder(root.rchild)def postorder(self, root):"""遞歸實(shí)現(xiàn)后續(xù)遍歷"""if root == None:returnself.postorder(root.lchild)self.postorder(root.rchild)print root.elem

根據(jù)數(shù)據(jù)畫樹圖

一定要中序：用來分割數(shù)據(jù)
前、后序：用來找根

樹的補(bǔ)充

只列出大綱，后序?qū)W習(xí)

二叉排序樹（BST）

平衡二叉樹（AVL）

特點(diǎn)：1.是二叉排序樹 ⒉滿足每個(gè)結(jié)點(diǎn)的平衡因子絕對值<=1

紅黑樹

紅黑樹是一個(gè)“適度平衡”的二叉搜索樹，而非如AVL一般“嚴(yán)格”的平衡。（說它不嚴(yán)格是因?yàn)樗皇菄?yán)格控制左、右子樹高度或節(jié)點(diǎn)數(shù)之差小于等于1。）
面試常問：什么是紅黑樹？

1.每個(gè)節(jié)點(diǎn)只能是紅色或者黑色。
2.根節(jié)點(diǎn)必須是黑色。
3.紅色節(jié)點(diǎn)的子節(jié)點(diǎn)只能是黑色。
4.從任一節(jié)點(diǎn)到其每個(gè)葉子節(jié)點(diǎn)，的所有路徑上，包含黑色節(jié)點(diǎn)的數(shù)目相同。

多路查找樹

B-樹（多路平衡查找樹）

視頻增刪查
B樹又稱為多路平衡查找樹，是一種組織和維護(hù)外存文件系統(tǒng)非常有效的數(shù)據(jù)結(jié)構(gòu)。比如數(shù)據(jù)庫的索引。

B+樹

b+樹和b樹的區(qū)別_B+樹和B/B樹的區(qū)別？Mysql為啥用B+樹來做索引？
b+樹適合范圍查找，比如找年齡在18-22歲的人的信息，先用隨機(jī)查找找到18，再用順序查到到22，速度極快，這也是為啥Mysql用B+樹來做索引。

主要區(qū)別：
1.所有關(guān)鍵字都會在在葉子節(jié)點(diǎn)出現(xiàn)
2.內(nèi)部節(jié)點(diǎn)(非葉子節(jié)點(diǎn))不存儲數(shù)據(jù)（b樹內(nèi)部節(jié)點(diǎn)是存儲data的），數(shù)據(jù)只在葉子節(jié)點(diǎn)存儲（葉子節(jié)指其下沒有子樹了）
3.所有葉子結(jié)點(diǎn)構(gòu)成了一個(gè)鏈指針，而且所有的葉子節(jié)點(diǎn)按照順序排列。

B+樹比B樹有什么優(yōu)勢？
1.每一層更寬，更胖，存儲的數(shù)據(jù)更多。因?yàn)锽+樹只存儲關(guān)鍵字，而不存儲多余data.所以B+樹的每一層相比B樹能存儲更多節(jié)點(diǎn)。
2.所有的節(jié)點(diǎn)都會在葉子節(jié)點(diǎn)上出現(xiàn)，查詢效率更穩(wěn)定。因?yàn)锽+樹節(jié)點(diǎn)上沒有數(shù)據(jù)，所以要查詢數(shù)據(jù)就必須到葉子節(jié)點(diǎn)上，所以查詢效率比B樹穩(wěn)定。而在 B 樹中，非葉子節(jié)點(diǎn)也會存儲數(shù)據(jù)，這樣就會造成查詢效率不穩(wěn)定的情況，有時(shí)候訪問到了非葉子節(jié)點(diǎn)就可以找到關(guān)鍵字，而有時(shí)需要訪問到葉子節(jié)點(diǎn)才能找到關(guān)鍵字。
3.查詢效率比B樹高。因?yàn)锽+樹更矮，更胖，所以和磁盤交互的次數(shù)比B樹更少，而且B+樹通過底部的鏈表也可以完成遍歷，但是B樹需要找到每個(gè)節(jié)點(diǎn)才能遍歷，所以B+樹效率更高。

總結(jié):
1.存的多 2.查詢穩(wěn)定 3.查的快

總結(jié)

以上是生活随笔為你收集整理的数据结构与算法（python版）的全部內(nèi)容，希望文章能夠幫你解決所遇到的問題。

如果覺得生活随笔網(wǎng)站內(nèi)容還不錯(cuò)，歡迎將生活随笔推薦給好友。