DeepLearning.AI第一部分第四周:深层神经网络
文章目錄
- 4.1深層神經網絡(Deep L-layer neural network)
- 4.2前向傳播和反向傳播(Forward and backward propagation)
- 4.3舉例說明前向傳播
- 4.4核對矩陣的維數(Getting your matrix dimensions right)
- 4.5(未檢查)為什么一般深層網絡比淺層網絡好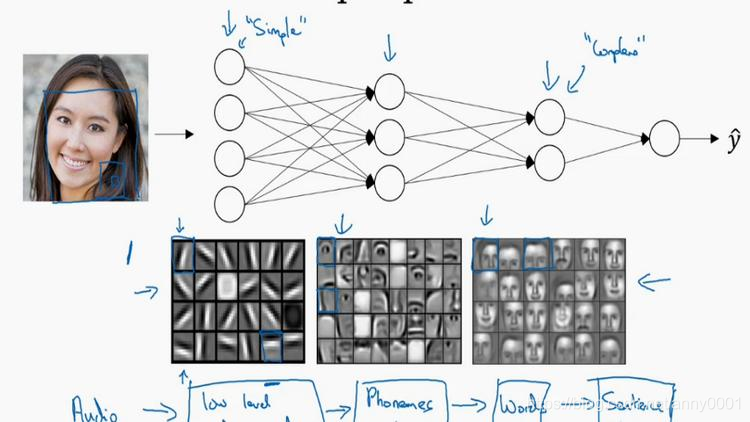
- 4.6 搭建神經網絡(看作業)
- 4.7 (未檢查)參數 VS 超參數(Parameters vs Hyperparameters)
- 4.8 深度學習和大腦的關聯性(What does this have to do with the brain?)
4.1深層神經網絡(Deep L-layer neural network)
接"DeepLearning.AI第一部分第三周"
上圖左邊是邏輯回歸,右邊是一個隱層的神經網絡。
上圖左邊是兩個隱藏層的神經網絡,右邊是五個隱藏層的神經網絡。嚴格上來說邏輯回歸也是一個一層的神經網絡,而上邊右圖一個深得多的模型,淺與深僅僅是指一種程度。記住以下要點:有一個隱藏層的神經網絡,就是一個兩層神經網絡。記住當我們算神經網絡的層數時,我們不算輸入層,我們只算隱藏層和輸出層。但是在過去的幾年中,DLI (深度學習學院 deep learning institute)已經意識到有一些函數,只有非常深的神經網絡能學會,而更淺的模型則辦不到。盡管對于任何給定的問題很難去提前預測到底需要多深的神經網絡,所以先去嘗試邏輯回歸,嘗試一層然后兩層隱含層,然后把隱含層的數量看做是另一個可以自由選擇大小的超參數,然后再保留交叉驗證數據上評估,或者用你的開發集來評估。
- 對于上圖的一些,符號定義:上圖是一個四層的神經網絡,有三個隱藏層。我們可以看到,第一層(即左邊數過去第二層,因為輸入層是第 0 層)有 5 個神經元數目,第二層 5 個,第三層 3 個。我們用 LLL 表示層數,上圖:L=4L = 4L=4,輸入層的索引為“0”,第一個隱藏層n[1]=5n^{[1]}=5n[1]=5,表示有 5個隱藏神經元,同理n[2]=5,n[3]=3,n[4]=n[L]=1n^{[2]} = 5,n^{[3]} = 3,n^{[4]} =n^{[L]} = 1n[2]=5,n[3]=3,n[4]=n[L]=1(輸出單元為 1)。而輸入層,n[0]=nx=3n^{[0]}=n_x = 3n[0]=nx?=3。在不同層所擁有的神經元的數目,對于每層 lll 都用a[l]a^{ [l]}a[l]來記作 lll 層激活后結果,我們會在后面看到在正向傳播時,最終會計算出a[l]a^{ [l]}a[l]。通過用激活函數 ggg 計算z[l]z^{[l]}z[l] ,激活函數也被索引為層數lll,然后我們用w[l]w^{[l]}w[l] 來記作在 lll 層計算z[l]z^{ [l]}z[l] 值的權重。類似的,計算z[l]z^{[l]}z[l] 的方程中的b[l]b^{[l]}b[l] 也一樣。最后總結下符號約定:輸入的特征記作xxx,但是xxx同樣也是 0 層的激活函數,所以x=a[0]x = a^{ [0]}x=a[0] 。最后一層的激活函數,所以a[L]a^{[L]}a[L] 是等于這個神經網絡所預測的輸出結果。
4.2前向傳播和反向傳播(Forward and backward propagation)
之前我們學習了構成深度神經網絡的基本模塊,比如每一層都有前向傳播步驟以及一個相反的反向傳播步驟,現在我們來談談如何實現這些步驟。先講前向傳播,輸入a[l?1]a^{[l?1]}a[l?1],輸出是a[l]a^{[l]}a[l],緩存為z[l]z^{[l]}z[l];從實現的角度來說我們可以緩存下w[l]w^{[l]}w[l] 和b[l]b^{ [l] }b[l],這樣更容易在不同的環節中調用函數。
所以前向傳播的步驟可寫成:
z[l]=W[l]a[l?1]+b[l]z^{[l]} = W^{[l]}a^{[l-1]}+b^{[l]}z[l]=W[l]a[l?1]+b[l],a[l]=g[l](z[l])a^{[l]}=g^{[l]}(z^{[l]})a[l]=g[l](z[l])
向量化實現過程可以寫成:
z[l]=W[l]?A[l?1]+b[l]z^{[l]} = W^{[l]} ? A^{ [l?1]} + b^{ [l]}z[l]=W[l]?A[l?1]+b[l]
A[l]=g[l](Z[l])A^{ [l]} = g^{ [l]}( Z^{ [l]} )A[l]=g[l](Z[l])
前向傳播需要喂入A[0]A^{ [0]}A[0] 也就是輸入XXX,來初始化第一層的輸入值。a[0]a^{ [0]}a[0] 對應于一個訓練樣本的輸入特征,而A[0]A^{ [0]}A[0] 對應于一整個訓練樣本的輸入特征,所以這就是這條鏈的第一個前向函數的輸入,重復這個步驟就可以從左到右計算前向傳播。
反向傳播的步驟:輸入為da[l]da^{ [l]}da[l],輸出為da[l?1]da^{ [l?1]}da[l?1],dw[l]dw^{ [l]}dw[l],db[l]db^{ [l]}db[l]
所以反向傳播的步驟可以寫成:
(1) dz[l]=da[l]?g[l]′(z[l])dz^{[l]} = da^{[l]} * g^{[l]}{'}(z^{[l]})dz[l]=da[l]?g[l]′(z[l])
(2) dw[l]=dz[l]?a[l?1]dw^{[l]} = dz^{[l]} \cdot a^{[l-1]}dw[l]=dz[l]?a[l?1]
(3) db[l]=dz[l]db^{[l]} = dz^{[l]}db[l]=dz[l]
(4) da[l?1]=(w[l])T?z[l]da^{[l-1]}={(w^{[l]})}^T \cdot z^{[l]}da[l?1]=(w[l])T?z[l]
(5) dz[l]=(w[l+1])T?dz[l+1]?(g[l])′(z[l])dz^{[l]} = (w^{[l+1]})^{T} \cdot dz^{[l+1]} \cdot (g^{[l]})^{'}(z^{[l]})dz[l]=(w[l+1])T?dz[l+1]?(g[l])′(z[l])
式子(5)由式子(4)帶入式子(1)得到,前四個式子就可以實現反響函數。其向量化實現過程可以寫成:
(6) dZ[l]=dA[l]?g[l]′(Z[l])dZ^{[l]} = dA^{[l]}*{g^{[l]}}{'}(Z^{[l]})dZ[l]=dA[l]?g[l]′(Z[l])
(7) dW[l]=1mdZ[l]?(A[l?1])TdW^{[l]} = \frac{1}{m}dZ^{[l]}\cdot (A^{[l-1]})^TdW[l]=m1?dZ[l]?(A[l?1])T
(8) db[l]=1mnp.sum(dz[l],axis=1,keepdims=True)db^{[l]} = \frac{1}{m}np.sum(dz^{[l]},axis=1,keepdims=True)db[l]=m1?np.sum(dz[l],axis=1,keepdims=True)
(9) dA[l?1]=(W[l])T?dZ[l]dA{[l-1]} = (W^{[l]})^{T} \cdot dZ^{[l]}dA[l?1]=(W[l])T?dZ[l]
第一層你可能有一個 ReLU 激活函數,第二層為另一個 ReLU 激活函數,第三層可能是sigmoid 函數(如果你做二分類的話),輸出值為,用來計算損失;這樣你就可以向后迭代進行反向傳播求導來求dw[3],db[3],dw[2],db[2],dw[1],db[1]dw^{ [3]},db^{[3]} ,dw^{ [2]} ,db^{ [2]} ,dw^{ [1]} ,db^{ [1]}dw[3],db[3],dw[2],db[2],dw[1],db[1] 。在計算的時候,緩存會把z[1]z[2]z[3]z^{ [1]} z^{ [2]} z^{ [3]}z[1]z[2]z[3] 傳遞過來,然后回傳da[2],da[1]da^{ [2]} , da^{ [1]}da[2],da[1] ,即一個三層網絡的前向和反向傳播。{還有一個細節沒講就是前向遞歸——用輸入數據來初始化,那么反向遞歸(使用 Logistic 回歸做二分類)——對A [l] 求導。}
4.3舉例說明前向傳播
4.4核對矩陣的維數(Getting your matrix dimensions right)
當實現深度神經網絡的時候,其中一個我常用的檢查代碼是否有錯的方法就是拿出一張紙過一遍算法中矩陣的維數。
www的維度是(下一層的維數,前一層的維數),即w[l]:(n[l],n[l?1])w^{[l]} : (n^{ [l]} ,n^{ [l?1]} )w[l]:(n[l],n[l?1]);
bbb的維度是(下一層的維數,1),即:b[l]:(n[l],1)b^{[l]} : (n^{ [l]} , 1)b[l]:(n[l],1);
z[l],a[l]:(n[l],1)z^{ [l]} ,a^{ [l]} : (n^{ [l]} , 1)z[l],a[l]:(n[l],1);
dw[l]dw^{ [l]}dw[l] 和w[l]w^{ [l]}w[l] 維度相同,db[l]db^{ [l]}db[l] 和b[l]b^{ [l]}b[l] 維度相同,且www和bbb向量化維度不變,但z,az,az,a以及xxx的維度會在向量化后發生變化。
向量化后:Z[l]Z^{[l]}Z[l] 可以看成由每一個單獨的Z[l]Z^{ [l]}Z[l] 疊加而得到, Z[l]=(z[l](1),z[l](2),z[l](3),...,z[l](m))Z^{ [l]} = (z^{[l](1)} , z^{[l](2)} , z^{ [l](3)} , ... , z^{ [l](m)} )Z[l]=(z[l](1),z[l](2),z[l](3),...,z[l](m)),mmm為訓練集大小,所以Z[l]Z^{ [l]}Z[l] 的維度不再是(n[l],1)(n^{ [l]} , 1)(n[l],1),而是(n[l],m)(n^{ [l]} , m)(n[l],m)。A[l]:(n[l],m),A[0]=X=(n[l],m)A^{[l]} :(n^{ [l]} , m),A^{ [0]} = X = (n^{ [l]} , m)A[l]:(n[l],m),A[0]=X=(n[l],m)
在做深度神經網絡的反向傳播時,一定要確認所有的矩陣維數是前后一致的,可以大大提高代碼通過率。下一節我們講為什么深層的網絡在很多問題上比淺層的好。
4.5(未檢查)為什么一般深層網絡比淺層網絡好
首先,深度網絡究竟在計算什么?如果你在建一個人臉識別或是人臉檢測系統,深度神經網絡所做的事就是,當你輸入一張臉部的照片,然后你可以把深度神經網絡的第一層,當成一個特征探測器或者邊緣探測器。在這個例子里,我會建一個大概有 20 個隱藏單元的深度神經網絡,是怎么針對這張圖計算的。隱藏單元就是這些圖里這些小方塊(第一張大圖),舉個例子,這個小方塊(第一行第一列)就是一個隱藏單元,它會去找這張照片里“|”邊緣的方向。那么這個隱藏單元(第四行第四列),可能是在找(“—”)水平向的邊緣在哪里。之后的課程里,我們會講專門做這種識別的卷積神經網絡,到時候會細講,為什么小單元是這么表示的。你可以先把神經網絡的第一層當作看圖,然后去找這張照片的各個邊緣。我們可以把照片里組成邊緣的像素們放在一起看,然后它可以把被探測到的邊緣組合成面部的不同部分(第二張大圖)。比如說,可能有一個神經元會去找眼睛的部分,另外還有別的在找鼻子的部分,然后把這許多的邊緣結合在一起,就可以開始檢測人臉的不同部分。最后再把這些部分放在一起,比如鼻子眼睛下巴,就可以識別或是探測不同的人臉(第三張大圖)。
你可以直覺上把這種神經網絡的前幾層當作探測簡單的函數,比如邊緣,之后把它們跟后幾層結合在一起,那么總體上就能學習更多復雜的函數。這些圖的意義,我們在學習卷積神經網絡的時候再深入了解。還有一個技術性的細節需要理解的是,邊緣探測器其實相對來說都是針對照片中非常小塊的面積。就像這塊(第一行第一列),都是很小的區域。面部探測器就會針對于大一些的區域,但是主要的概念是,一般你會從比較小的細節入手,比如邊緣,然后再一步步到更大更復雜的區域,比如一只眼睛或是一個鼻子,再把眼睛鼻子裝一塊組成更復雜的部分。
這種從簡單到復雜的金字塔狀表示方法或者組成方法,也可以應用在圖像或者人臉識別以外的其他數據上。比如當你想要建一個語音識別系統的時候,需要解決的就是如何可視化語音,比如你輸入一個音頻片段,那么神經網絡的第一層可能就會去先開始試著探測比較低層次的音頻波形的一些特征,比如音調是變高了還是低了,分辨白噪音,咝咝咝的聲音,或者音調,可以選擇這些相對程度比較低的波形特征,然后把這些波形組合在一起就能去探測聲音的基本單元。在語言學中有個概念叫做音位,比如說單詞 ca,c 的發音,“嗑”就是一個音位,a 的發音“啊”是個音位,t 的發音“特”也是個音位,有了基本的聲音單元以后,組合起來,你就能識別音頻當中的單詞,單詞再組合起來就能識別詞組,再到完整的句子。
所以深度神經網絡的這許多隱藏層中,較早的前幾層能學習一些低層次的簡單特征,等到后幾層,就能把簡單的特征結合起來,去探測更加復雜的東西。比如你錄在音頻里的單詞、詞組或是句子,然后就能運行語音識別了。同時我們所計算的之前的幾層,也就是相對簡單的輸入函數,比如圖像單元的邊緣什么的。到網絡中的深層時,你實際上就能做很多復雜的事,比如探測面部或是探測單詞、短語或是句子。
- Small:隱藏單元的數量相對較少
- Deep:隱藏層數目比較多
深層的網絡隱藏單元數量相對較少,隱藏層數目較多,如果淺層的網絡想要達到同樣的計算結果則需要指數級增長的單元數量才能達到。
另外一個,關于神經網絡為何有效的理論,來源于電路理論,它和你能夠用電路元件計算哪些函數有著分不開的聯系。根據不同的基本邏輯門,譬如與門、或門、非門。在非正式的情況下,這些函數都可以用相對較小,但很深的神經網絡來計算,小在這里的意思是隱藏單元的數量相對比較小,但是如果你用淺一些的神經網絡計算同樣的函數,也就是說在我們不能用很多隱藏層時,你會需要成指數增長的單元數量才能達到同樣的計算結果。
再來舉個例子,用沒那么正式的語言介紹這個概念。假設你想要對輸入特征計算異或或是奇偶性,你可以算x 1 XORx 2 XORx 3 XOR … … x n ,假設你有n或者n x 個特征,如果你畫一個異或的樹圖,先要計算x 1 ,x 2 的異或,然后是x 3 和x 4 。技術上來說如果你只用或門,還有非門的話,你可能會需要幾層才能計算異或函數,但是用相對小的電路,你應該就可以計算異或了。然后你可以繼續建這樣的一個異或樹圖(上圖左),那么你最后會得到這樣的電路^ = y,也就是輸入特征的異或,或是奇偶性,要計算異或關系。這種樹圖對來輸出結果y,y應網絡的深度應該是O(log(n)),那么節點的數量和電路部件,或是門的數量并不會很大,你也不需要太多門去計算異或。
但是如果你不能使用多隱層的神經網絡的話,在這個例子中隱層數為O(log(n)),比如你被迫只能用單隱藏層來計算的話,這里全部都指向從這些隱藏單元到后面這里,再輸出y,那么要計算奇偶性,或者異或關系函數就需要這一隱層(上圖右方框部分)的單元數呈指數增長才行,因為本質上來說你需要列舉耗盡2 n 種可能的配置,或是2 n 種輸入比特的配置。異或運算的最終結果是 1 或 0,那么你最終就會需要一個隱藏層,其中單元數目隨輸入比特指數上升。精確的說應該是2 n?1 個隱藏單元數,也就是O(2 n )。
我希望這能讓你有點概念,意識到有很多數學函數用深度網絡計算比淺網絡要容易得多,我個人倒是認為這種電路理論,對訓練直覺思維沒那么有用,但這個結果人們還是經常提到的,用來解釋為什么需要更深層的網絡。除了這些原因,說實話,我認為“深度學習”這個名字挺唬人的,這些概念以前都統稱為有很多隱藏層的神經網絡,但是深度學習聽起來多高大上,太深奧了,對么?這個詞流傳出去以后,這是神經網絡的重新包裝或是多隱藏層神經網絡的重新包裝,激發了大眾的想象力。拋開這些公關概念重新包裝不談,深度網絡確實效果不錯,有時候人們還是會按照字面意思鉆牛角尖,非要用很多隱層。但是當我開始解決一個新問題時,我通常會從 logistic 回歸開始,再試試一到兩個隱層,把隱藏層數量當作參數、超參數一樣去調試,這樣去找比較合適的深度。但是近幾年以來,有一些人會趨向于使用非常非常深邃的神經網絡,比如好幾打的層數,某些問題中只有這種網絡才是最佳模型。
4.6 搭建神經網絡(看作業)
4.7 (未檢查)參數 VS 超參數(Parameters vs Hyperparameters)
想要你的深度神經網絡起很好的效果,你還需要規劃好你的參數以及超參數。
什么是超參數?
比如算法中的 learning rate α\alphaα(學習率)、iterations(梯度下降法循環的數量)、L(隱藏層數目)、n[l]n^{ [l]}n[l] (隱藏層單元數目)、choice of activation function(激活函數的選擇)都需要
你來設置,這些數字實際上控制了最后的參數W和b的值,所以它們被稱作超參數。
實際上深度學習有很多不同的超參數,之后我們也會介紹一些其他的超參數,如momentum、mini batch size、regularization parameters 等等。
今天的深度學習應用領域,還是很經驗性的過程,通常你有個想法,比如你可能大致知道一個最好的學習率值,可能說a = 0.01最好,我會想先試試看,然后你可以實際試一下,訓練一下看看效果如何。然后基于嘗試的結果你會發現,你覺得學習率設定再提高到 0.05 會
比較好。如果你不確定什么值是最好的,你大可以先試試一個學習率a,再看看損失函數 J
的值有沒有下降。然后你可以試一試大一些的值,然后發現損失函數的值增加并發散了。然
后可能試試其他數,看結果是否下降的很快或者收斂到在更高的位置。你可能嘗試不同的a
并觀察損失函數J這么變了,試試一組值,然后可能損失函數變成這樣,這個a值會加快學習
過程,并且收斂在更低的損失函數值上(箭頭標識),我就用這個a值了。
在前面幾頁中,還有很多不同的超參數。然而,當你開始開發新應用時,預先很難確切
知道,究竟超參數的最優值應該是什么。所以通常,你必須嘗試很多不同的值,并走這個循
環,試試各種參數。試試看 5 個隱藏層,這個數目的隱藏單元,實現模型并觀察是否成功,
然后再迭代。這頁的標題是,應用深度學習領域,一個很大程度基于經驗的過程,憑經驗的
過程通俗來說,就是試直到你找到合適的數值。
另一個近來深度學習的影響是它用于解決很多問題,從計算機視覺到語音識別,到自然
語言處理,到很多結構化的數據應用,比如網絡廣告或是網頁搜索或產品推薦等等。我所看
到過的就有很多其中一個領域的研究員,這些領域中的一個,嘗試了不同的設置,有時候這
種設置超參數的直覺可以推廣,但有時又不會。所以我經常建議人們,特別是剛開始應用于
新問題的人們,去試一定范圍的值看看結果如何。然后下一門課程,我們會用更系統的方法,
用系統性的嘗試各種超參數取值。然后其次,甚至是你已經用了很久的模型,可能你在做網
絡廣告應用,在你開發途中,很有可能學習率的最優數值或是其他超參數的最優值是會變的,
所以即使你每天都在用當前最優的參數調試你的系統,你還是會發現,最優值過一年就會變
化,因為電腦的基礎設施,CPU 或是 GPU 可能會變化很大。所以有一條經驗規律可能每幾
個月就會變。如果你所解決的問題需要很多年時間,只要經常試試不同的超參數,勤于檢驗
結果,看看有沒有更好的超參數數值,相信你慢慢會得到設定超參數的直覺,知道你的問題
最好用什么數值。
這可能的確是深度學習比較讓人不滿的一部分,也就是你必須嘗試很多次不同可能性。
但參數設定這個領域,深度學習研究還在進步中,所以可能過段時間就會有更好的方法決定
超參數的值,也很有可能由于 CPU、GPU、網絡和數據都在變化,這樣的指南可能只會在一
段時間內起作用,只要你不斷嘗試,并且嘗試保留交叉檢驗或類似的檢驗方法,然后挑一個
對你的問題效果比較好的數值。
近來受深度學習影響,很多領域發生了變化,從計算機視覺到語音識別到自然語言處理到很多結構化的數據應用,比如網絡廣告、網頁搜索、產品推薦等等;有些同一領域設置超
參數的直覺可以推廣,但有時又不可以,特別是那些剛開始研究新問題的人們應該去嘗試一
定范圍內的結果如何,甚至那些用了很久的模型得學習率或是其他超參數的最優值也有可能
會改變。
在下個課程我們會用系統性的方法去嘗試各種超參數的取值。有一條經驗規律:經常試
試不同的超參數,勤于檢查結果,看看有沒有更好的超參數取值,你將會得到設定超參數的
直覺。
4.8 深度學習和大腦的關聯性(What does this have to do with the brain?)
深度學習和大腦有什么關聯性嗎?
關聯不大。
那么人們為什么會說深度學習和大腦相關呢?
當你在實現一個神經網絡的時候,那些公式是你在做的東西,你會做前向傳播、反向傳
播、梯度下降法,其實很難表述這些公式具體做了什么,深度學習像大腦這樣的類比其實是
過度簡化了我們的大腦具體在做什么,但因為這種形式很簡潔,也能讓普通人更愿意公開討
論,也方便新聞報道并且吸引大眾眼球,但這個類比是非常不準確的。
一個神經網絡的邏輯單元可以看成是對一個生物神經元的過度簡化,但迄今為止連神經
科學家都很難解釋究竟一個神經元能做什么,它可能是極其復雜的;它的一些功能可能真的
類似 logistic 回歸的運算,但單個神經元到底在做什么目前還沒有人能夠真正可以解釋。
深度學習的確是個很好的工具來學習各種很靈活很復雜的函數,學習到從x到y的映射,
在監督學習中學到輸入到輸出的映射。
但這個類比還是很粗略的,這是一個 logistic 回歸單元的 sigmoid 激活函數,這里是一
個大腦中的神經元,圖中這個生物神經元,也是你大腦中的一個細胞,它能接受來自其他神
經元的電信號,比如x 1 , x 2 , x 3 ,或可能來自于其他神經元a 1 , a 2 , a 3 。其中有一個簡單的臨界
計算值,如果這個神經元突然激發了,它會讓電脈沖沿著這條長長的軸突,或者說一條導線傳到另一個神經元。
所以這是一個過度簡化的對比,把一個神經網絡的邏輯單元和右邊的生物神經元對比。
至今為止其實連神經科學家們都很難解釋,究竟一個神經元能做什么。一個小小的神經元其
實卻是極其復雜的,以至于我們無法在神經科學的角度描述清楚,它的一些功能,可能真的
是類似 logistic 回歸的運算,但單個神經元到底在做什么,目前還沒有人能夠真正解釋,大
腦中的神經元是怎么學習的,至今這仍是一個謎之過程。到底大腦是用類似于后向傳播或是
梯度下降的算法,或者人類大腦的學習過程用的是完全不同的原理。
所以雖然深度學習的確是個很好的工具,能學習到各種很靈活很復雜的函數來學到從 x
到 y 的映射。在監督學習中,學到輸入到輸出的映射,但這種和人類大腦的類比,在這個領
域的早期也許值得一提。但現在這種類比已經逐漸過時了,我自己也在盡量少用這樣的說法。
這就是神經網絡和大腦的關系,我相信在計算機視覺,或其他的學科都曾受人類大腦啟
發,還有其他深度學習的領域也曾受人類大腦啟發。但是個人來講我用這個人類大腦類比的
次數逐漸減少了。
總結
以上是生活随笔為你收集整理的DeepLearning.AI第一部分第四周:深层神经网络的全部內容,希望文章能夠幫你解決所遇到的問題。

- 上一篇: 打包python程序
- 下一篇: 源码安装sippyqt4 for ubu
