函数的定义域
前言
“皮之不存,毛將焉附”,函數的定義域是函數及其性質存在的基礎和依托;函數的定義說“函數是非空數集到非空數集的映射”,第一個非空數集就是定義域。所以一提起函數及其性質,我們往往先想到的就是函數的定義域。如果一個函數的定義域是空集,那么這個函數即使給出了所謂的解析式,也是空函數,沒有研究的價值,因此數學老師常常強調的一句話就是“定義域優先”。
不同形式
自然定義域,比如給定(g(x)=ln(x-1)),則使得解析式有意義的值都屬于定義域,即解(x-1>0)得到定義域為((1,+infty));
限定定義域,比如已知函數(f(x)=2x^2-3sinx),(xin [0,cfrac{pi}{2}]),則這就是限定定義域;
實際問題定義域,比如線段長度為(x),則至少必須滿足(x>0);
給出方式
1、直接給出(限定定義域);如函數(f(x),xin D)
2、以函數解析式的形式給出(自然定義域);如已知函數(f(x)=lgcfrac{x+2}{x-2}),求其定義域;要知道這個函數的定義域,我們自然需要解不等式(cfrac{x+2}{x-2}>0),由穿針引線法可得定義域為(x)(in)((-infty,-2))(cup)((2,+infty))。
3、以圖像的形式給出,如圖所示,函數圖像向(x)軸作正射影,就得到定義域;
向(y)軸作正射影,就得到值域。當然,你如果會用圖像,那么由此圖像還可以解不等式(f(x)>0)或(f(x)leq 0)
4、以實際問題給出,比如(x)為某個線段的長度,則隱含(xge 0),自然就不能取負值的。
求定義域
如果給定函數解析式,求定義域,轉化為解不等式(組);
已知函數(f(x)=cfrac{sqrt{x^2-1}}{ln(x-1)}),求其定義域;
分析:要使得解析式有意義,須滿足(egin{cases}x^2-1ge 0\x-1>0\ln(x-1)
eq 0end{cases}),從而解得({xmid x>1且x
eq 2}),即定義域為((1,2)cup(2,+infty)).
復合函數的定義域
已知函數(f(x))的定義域是([-1,1]),求函數(f(2x+1))的定義域;
分析:解決這類題目需要牢牢抓住兩點:其一接受對應法則(f)作用的(x)和(2x+1)是處于對等位置的,
其二不論是給定函數的定義域還是求解函數的定義域,都是針對單獨的自變量(x)而言,
據此可知由于(-1leq xleq 1),故(-1leq 2x+1leq 1),解得函數(f(2x+1))的定義域是(xin [-1,0])。
已知函數(f(x)=lgcfrac{x+2}{2-x}),求函數(f(cfrac{x}{2})+f(cfrac{2}{x}))的定義域;
分析:由上知,函數(f(x))的定義域為(xin(-2,2)),故和自變量(x)對等的(cfrac{x}{2})和(cfrac{2}{x})也必須在這個范圍內,
則有(egin{cases} -2<cfrac{x}{2}<2 \ -2<cfrac{2}{x}<2 end{cases}),解得(xin (-4,-1)cup(1,4))。
已知函數(f(x+1))的定義域是([0,1]),求函數(f(2^x-2))的定義域。
分析:這里同樣你得清楚(x+1)和(2^x-2)是對等的,先由(xin[0,1]),
計算得到(1leq x+1leq 2),故(1leq 2^x-2leq 2),
解得(3leq 2^xleq 4),同時取以2為底的對數得到(log_2^3leq xleq 2),
則所求定義域是(xin [log_2^3,2])。
分段函數的定義域
已知函數(f(x)=egin{cases}x^2+4x,&xge0\4x-x^2,&x<0end{cases}),求其定義域;
分析:分段函數的定義域是各段函數的定義域的并集,當然值域也是各段函數的值域的并集;
抽象函數的定義域(往往和復合函數不分家)
已知函數(f(2x+1))的定義域是([-1,1]),求函數(f(x))的定義域;
分析:由上面的例子分析可知,所給函數的定義域是([-1,1]),即函數(f(2x+1))的自變量(x)的取值范圍是([-1,1]),
故內函數(2x+1)的取值范圍這樣求解,由(-1leq x leq 1),得到(-2leq 2x leq 2),
所以(-1=-2+1leq 2x+1 leq 2+1=3),又由于(2x+1)和(x)對等(你可以理解為這兩個接受同樣的紀律約束也行),
所以(f(x))的(x)的取值范圍應該是(-1leq xleq 3),故函數(f(x))的定義域是([-1,3])。
【2019屆高三理科函數及其表示課時作業第15題】已知函數(f(x^2-3)=lgcfrac{x^2}{x^2-4}),則(f(x))的定義域為____________。
分析:本題目的定義域求解應該考慮兩層要求,
其一需要解析式(lgcfrac{x^2}{x^2-4})有意義,
即(cfrac{x^2}{x^2-4}>0),解得(x<-2)或(x>2①);
其二,令(x^2-3=t),則(tge -3),則(x^2=t+3),(x^2-4=t-1),
故原函數可以改寫為(f(t)=lgcfrac{t+3}{t-1}(tge -3)),
即(f(x)=lgcfrac{x+3}{x-1}(xge -3)),
則在(xge -3)時,還必須(cfrac{x+3}{x-1}>0),解得(x<-3)或(x>1),
故所求定義域必須同時滿足條件
(left{egin{array}{l}{x<-2,x>2}\{xge -3}\{x<-3,x>1}end{array}ight.),故定義域為(x>2),即((2,+infty));
總結:上述的解法是錯誤的,原因是解析式右端(lgcfrac{x^2}{x^2-4})中的(x)與(f(x))中的(x)的內涵不一樣,
(f(x))中的(x)與(f(x^2-3))中的(x^2-3)的整體是對等的,故需要先等價轉化得到函數的解析式。
【正解】令(x^2-3=t),則(tge -3),則(x^2=t+3),(x^2-4=t-1),
故原函數可以改寫為(f(t)=lgcfrac{t+3}{t-1}(tge -3)),
即(f(x)=lgcfrac{x+3}{x-1}(xge -3)),
則在(xge -3)時,還必須(cfrac{x+3}{x-1}>0),解得(x<-3)或(x>1),
故所求定義域必須同時滿足條件
(left{egin{array}{l}{xge -3}\{x<-3,x>1}end{array}ight.),故定義域為(x>1),即((1,+infty));
三角函數定義域
【求三角不等式和其他不等式的交集】求函數(f(x)=sqrt{5-|x|}+log_a(sinx-cfrac{1}{2}))的定義域。
分析:由題目可知,(|x|leq 5①),且(sinx>cfrac{1}{2}②)
解①得到(-5leq xleq 5);解②得到(2kpi+cfrac{pi}{6}<x<2kpi+cfrac{5pi}{6}(kin Z)),
二者求交集,如右圖所示,
得到定義域為([-5,-cfrac{7pi}{6})cup (cfrac{pi}{6},cfrac{5pi}{6}))。
影響要素
當函數的圖像發生變換時,其定義域和值域常常會隨之發生變化,舉例說明如下:
比如已知函數(f(x))的定義域是([1,5]),則(xin [1,5])
平移變換:則(f(x+2))的定義域就變成了([-1,3]),原因是(1leq x+2leq 5),解得(xin [-1,3]);
伸縮變換:則(2f(x))的定義域不做變化。
周期變換:則(f(2x))的定義域就變成了([cfrac{1}{2},cfrac{5}{2}]),原因是(1leq 2xleq 5),解得(xin[cfrac{1}{2},cfrac{5}{2}]);
易錯警示
當題目中明確要求定義域時,一般學生都不會出錯,但是在解題中學生又非常容易犯錯誤,主要原因還是缺乏定義域優先考慮的意識。一般來說,只要是研究函數的問題,不管題目是否要求我們求解定義域,都應該先確定函數的定義域,否則研究的函數就是無源之水,無本之木。
【2017鳳翔中學高三理科第二次月考第9題】若函數(f(x)=log_a^;(6-ax))在([0,2])上為減函數,則實數(a)的取值范圍是【】
$A.[3,+infty)$ $B.(0,1)$ $C.(1,3]$ $D.(1,3)$
分析:令(g(x)=6-ax),像這類題目既要考慮單調性,還要考慮定義域,學生常犯的錯誤就是只考慮單調性而不顧及定義域。
由題目可知必有(a>0),故函數(g(x))單調遞減,考慮定義域時只要最小值(g(2)>0)即可,解得(6-2a>0),即(a<3),
再考慮外函數必須是增函數,故(a>1),綜上可知,解得(1<a<3),故選(D)。
引申:原題目改為在([0,2))上為減函數,則實數(a)的取值范圍是(ain (1,3])。
典例剖析
如果題目給出了函數的定義域,那么這時往往會轉而求函數的其他性質,或者將已知的定義域轉化為其他的命題。
【已知定義域為(R)求參數的取值范圍】已知函數(f(x)=cfrac{mx-1}{mx^2+4mx+3})的定義域為(R),求(m)的取值范圍;
分析:由題可知,分母函數(y=mx^2+4mx+3
eq 0)對任意(xin R)都成立,分類討論如下:
①當(m=0)時,(y=3
eq 0)對任意(xin R)恒成立,故滿足題意;
②當(m
eq 0)時,結合分母函數的圖像可知,必須滿足(left{egin{array}{l}{m>0}\{Delta <0}end{array}ight.),
即(left{egin{array}{l}{m>0}\{Delta=(4m)^2-4 imes 3m<0}end{array}ight.),解得(0<m<cfrac{3}{4});
綜上所述,(m)的取值范圍為([0,cfrac{3}{4}));
<!------
【已知定義域或值域為$R$求參數的取值范圍】已知函數$f(x)=ln(x^2+2ax-a)$,
①如果函數的定義域是$R$,求參數$a$的取值范圍;
預備:先想一想,這個函數的定義域應該怎么求解?
分析:由于函數的定義域是$R$,說明對任意的$xin R$,都能使得$g(x)=x^2+2ax-a>0$,
轉化為二次函數恒成立問題了,(此時至少可以考慮數形結合或者恒成立分離參數)
這里用數形結合,函數$g(x)$開口向上,和$x$軸沒有交點,則$Delta <0$,
即$Delta=(2a)^2-4 imes 1 imes(-a)<0$,解得$ain (-1,0)$。
②如果函數的值域是$R$,求參數$a$的取值范圍;
分析:如右圖所示,要使得函數$f(x)$的值域是$R$,說明內函數$g(x)=x^2+2ax-a$必須要能取遍所有的正數,結合下圖,
如果有一部分正實數不能取到,那么函數$f(x)$的值域就不會是$R$,這樣只能是函數$g(x)$的$Delta ge 0$,
而不能是$Delta <0$,注意現在題目要求是值域為$R$,而不是定義域為$R$,
因此必須滿足條件$Delta=(2a)^2-4 imes 1 imes(-a)ge 0$,解得$ain {amid aleq -1 ,age 0}$。
下圖是參數$ain [-3,3]$時的兩個函數圖像的動態變化情況;
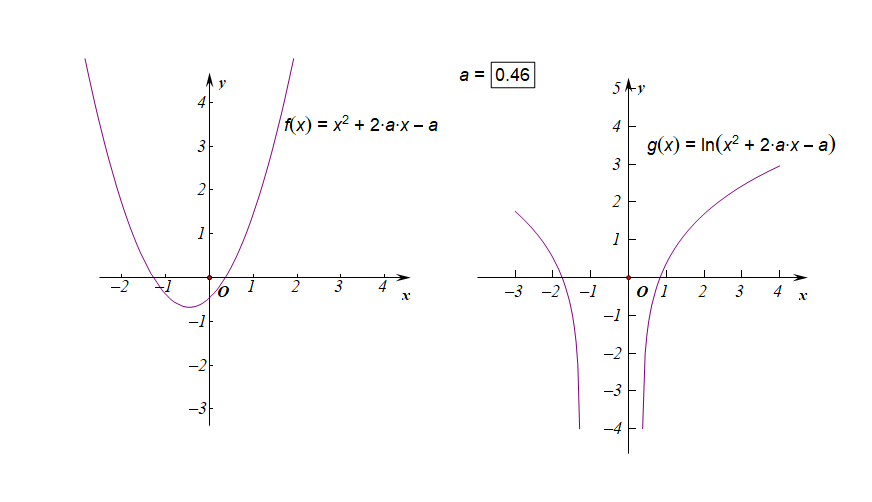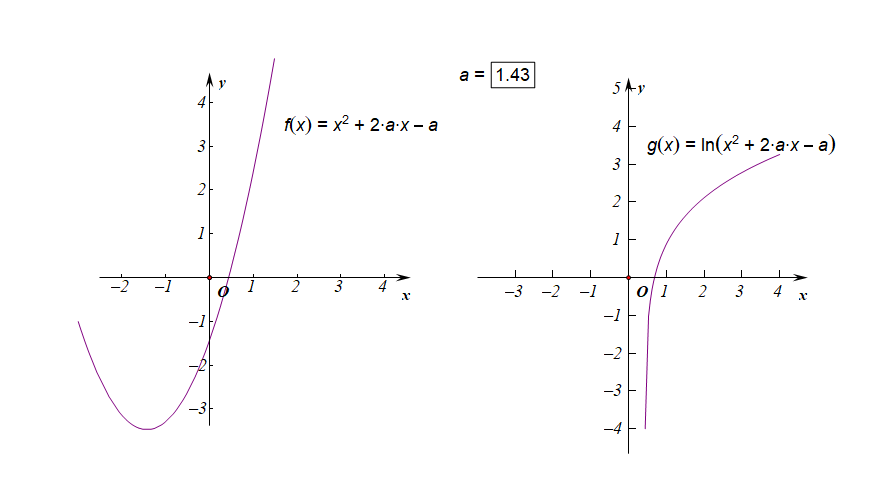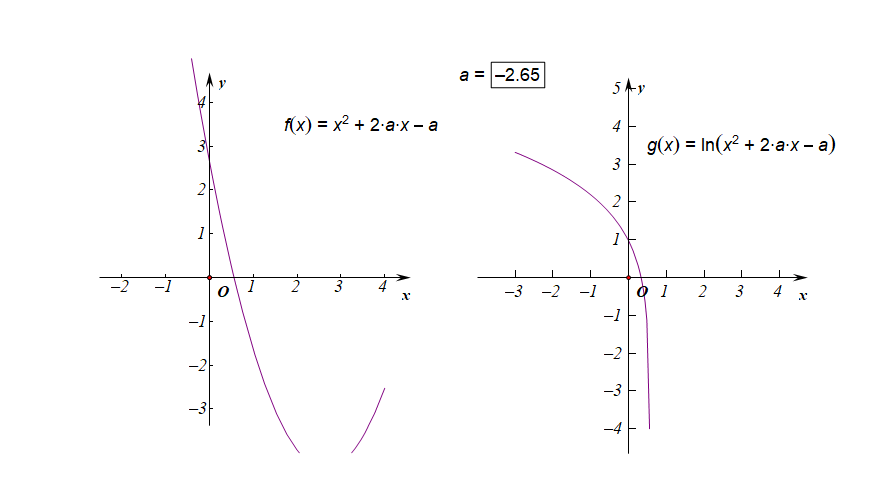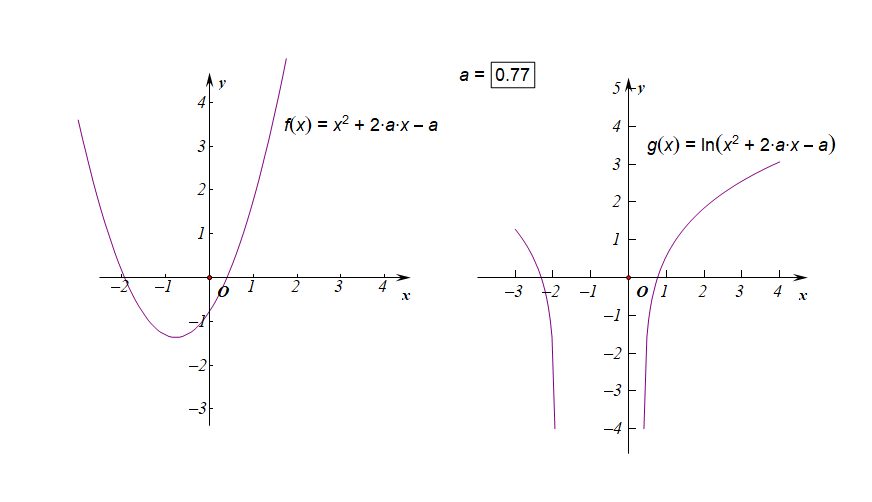
下圖是參數$ain (-1,0)$時的兩個函數圖像的動態變化情況;
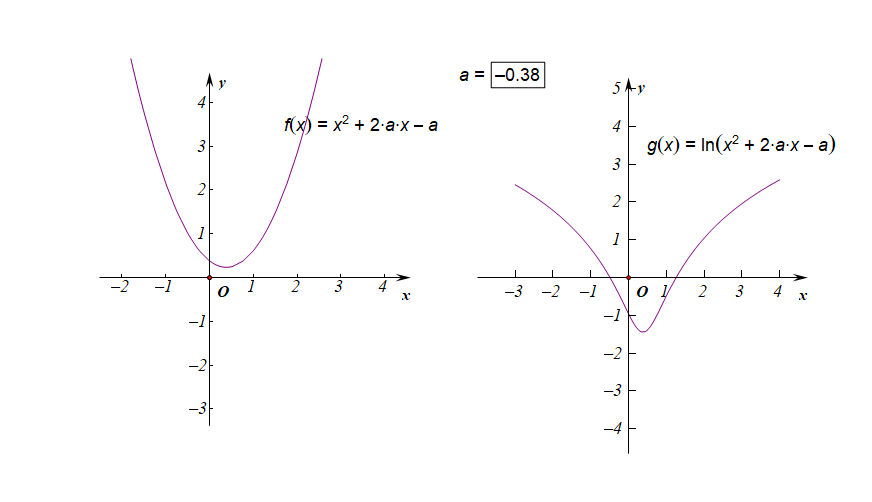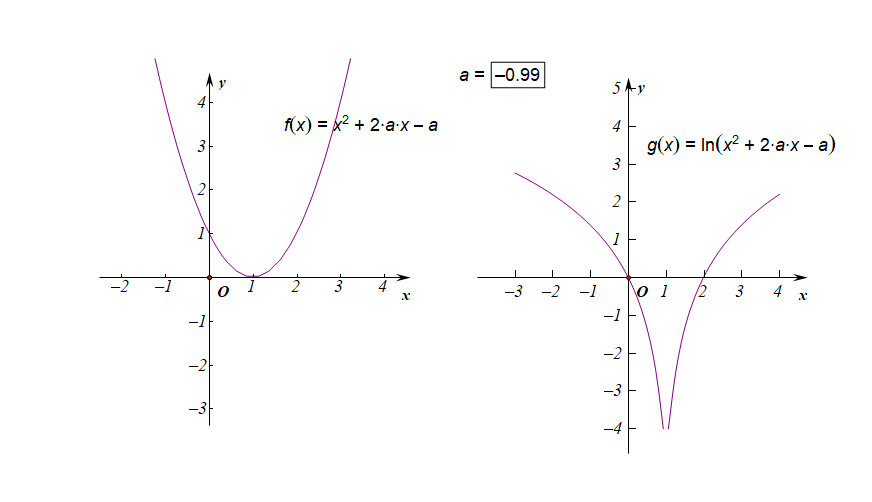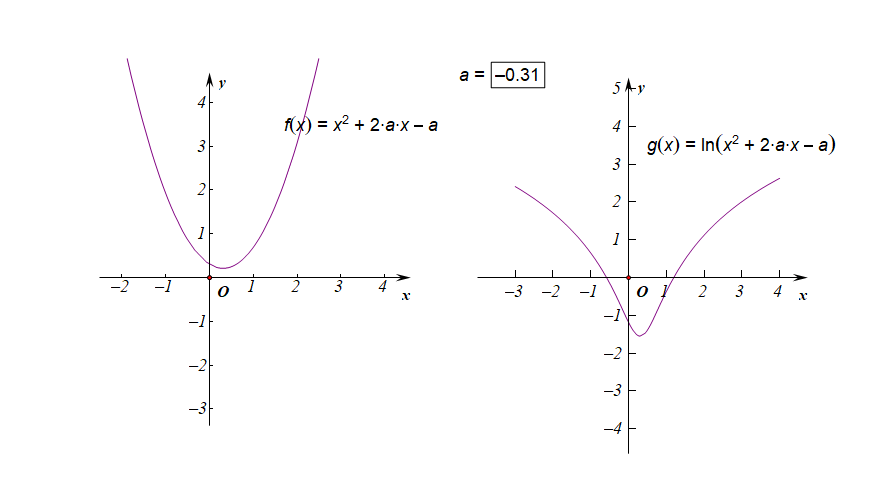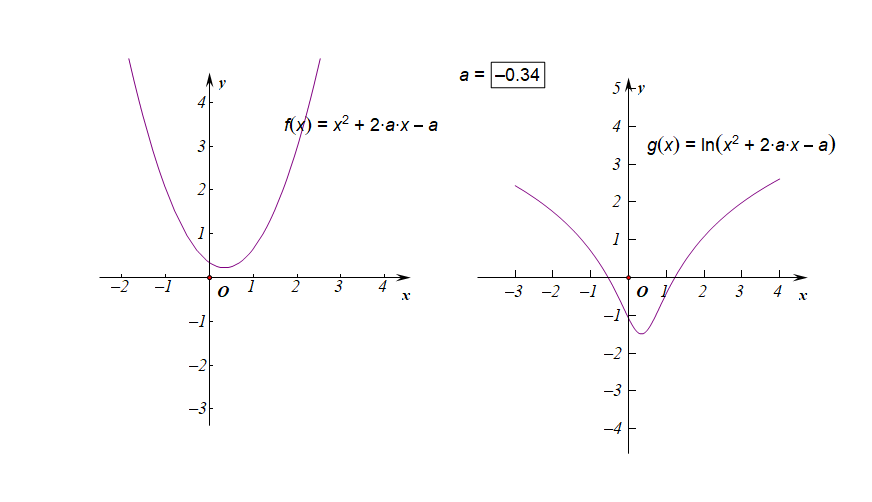
函數$y=lg(x^2-2x+a)$的值域不可能是【】
$A.(-infty,0]$ $B.[0,+infty)$ $C.[1,+infty)$ $D.R$
分析:對照右下圖可知,若參數$a$的取值能使得函數$g(x)=x^2-2x+a$取遍所有的正實數,
則函數$y=lgg(x)=lg(x^2-2x+a)$的值域為$R$,若不能取遍取遍所有的正實數,
則其值域可能為$[0,+infty)$或者$[1,+infty)$,但是就是不可能為$(-infty,0]$,故選$A$。
----->
【2016南京模擬】(f(x))是定義在((0,+infty))上的單調增函數,滿足(f(xy)=f(x)+f(y)),(f(3)=1),當(f(x)+f(x-8)leq 2)時,求(x)的取值范圍。
分析:(f(3)+f(3)=f(3 imes3)=f(9)=2), (f(x)+f(x-8)=f[x(x-8)]leq 2=f(9)),
等價轉化為(egin{cases}x>0\x-8>0\x(x-8)leq 9end{cases}), 解得(8<xleq 9).
易錯: 如果 (f(x)+f(x-8)=f[x(x-8)]leq 2=f(9)),轉化得到(egin{cases}x(x-8)>0\x(x-8)leq 9end{cases}),這樣的轉化往往是不等價的,因為(x(x-8)>0)包含了(x>0,x-8>0)和(x<0,x-8<0)兩種情形,由此我們得到的經驗是求定義域是一般對函數的形式不做變形,
因為我們大多做不到等價變形;比如給定函數(y=lgx^2),我們常常會化為(y=2lgx),殊不知這樣的變形是錯誤的,(y=lgx^2)的定義域是((-infty,0)cup(0,+infty)),還是偶函數,而(y=2lgx)的定義域是((0,+infty)),沒有奇偶性,其實(y=lgx^2=2lg|x|),有人就納悶了,我們平時不是經常用公式(log_a;b^n=nlog_a;b),對,沒錯,但是你注意過公式中的字母取值嗎?
總結

- 上一篇: Debian下搭建Samba CTDB集
- 下一篇: android视频教程
